Juros simples e Juros Composto
Publicado originalmente
Por Robson Luiz Mundo Educação
Juros simples
O juros simples é calculado com base em um valor fixado chamado de capital inicial. Trata-se de uma porcentagem do capital inicial aplicada durante determinado tempo. A principal característica do juros simples é que o valor não se altera no decorrer dos meses.
O conceito de juros simples é muito importante, uma vez que, em nosso cotidiano, ele é utilizado, por exemplo, na compra de algo parcelado ou em um empréstimo.
Fórmula do juros simples
A fórmula do juros simples é dada por:
Juros = capital · taxa · tempo
| J = C · i · t |
Para deduzir e justificar essa fórmula, vamos imaginar a seguinte situação-problema. Na compra de um produto no valor de R$ 100, o comprador solicitou o parcelamento em quatro vezes, entretanto, ao parcelar o valor do produto, é cobrada uma taxa de 1% ao mês.
Inicialmente, calcularemos 1% de 100.
1% de 100
0,01 · 100 = 1
– Mês 1:
Será cobrado o juros de 1 real, logo, o saldo devedor nesse primeiro mês será de:
100 + 1
– Mês 2:
Será cobrado novamente o juros de 1 real, assim, o saldo devedor será de:
100 + 1 +1
100 + 1 · 2
– Mês 3:
Será cobrado o juros de 1 real novamente, assim:
100 + 1 + 1 +1
100 + 1 · 3
– Mês 4:
Será cobrado, novamente, o juros de 1 real, assim:
100 + 1 + 1 + 1 + 1
100 + 1 · 4
104
Logo, o valor a ser pago ao final do parcelamento é de 104 reais.
Observando a situação-problema, veja que, à medida que o tempo passa, o juros é acrescido no valor do mês passado, ou seja: passados dois meses, o valor a ser pago é duas vezes o valor da taxa de juros; passados três meses, o valor a ser pago é três vezes o valor da taxa de juros, e assim sucessivamente.
De modo geral, após determinado tempo t (anos, meses, dias etc.), o valor a ser pago é de t vezes o valor da taxa de juros (i) e, claro, com base no capital inicial (C).
Tal afirmação, utilizando uma notação matemática, chega à fórmula apresentada anteriormente:
Juros = capital · taxa · tempo
| J = C · i · t |
Devemos ficar atentos à seguinte observação, a taxa de juros é sempre dada em porcentagem, mas, para realizar o cálculo, devemos utilizar a porcentagem em sua forma fracionária ou decimal.
Outro detalhe ao qual devemos atentar-nos são as unidades de medida do tempo e da taxa, elas devem estar sempre na mesma unidade, ou seja, se o tempo for dado em meses, a taxa de juros também deve ser dada em meses.
O montante (M) é o valor do capital inicial adicionado ao valor do juros, ou seja:
| M = C + J |
Como calcular juros simples
Para calcularmos o juros simples, basta substituir as informações dadas pelo problema na fórmula já deduzida. Para isso, vamos conferir algumas situações-problemas.
-
Exemplo 1
Ao investir R$ 3.000 em uma aplicação bancária sob o regime de juros simples, a uma taxa de 10% ao ano durante seis meses, qual o valor a ser retirado ao fim dessa aplicação?
O primeiro passo é anotar cada um dos dados do problema:
J = ?; C = 3000,00; i = 10% ao ano; e t = 6 meses
Agora, devemos observar as unidades de medida da taxa e do tempo. Caso estejam sendo utilizadas as mesmas unidades, basta substituí-las na fórmula. Caso contrário, temos que achar uma maneira de deixá-las iguais.
De modo geral, é mais fácil “transformar” a unidade de medida do tempo do que a da taxa, assim, vamos transformar 6 meses em anos, uma vez que a taxa foi dada em ano. Sabemos que temos 12 meses em um ano, logo, em meio ano, temos 6 meses.
0,5 ano → 6 meses
t = 0,5 ano
Passando a taxa de juros para a forma decimal, temos:
i = 10%
i = 10 ÷ 100
i = 0,1
Substituindo os dados na fórmula, temos:
J = C · i · t
J = 3000 · 0,1 · 0,5
J = 300 · 0,5
J = 150 reais
O juros, ao final da aplicação, é de 150 reais. Foi pedido o valor a ser retirado da aplicação, ou seja, o valor aplicado mais o juros (montante).
M = C + J
M = 3000 + 150
M = 3.150 reais
Logo, o valor a ser retirado da aplicação é de 3.150 reais.
Leia também: Multiplicação de números decimais: como calcular?
-
Exemplo 2
Determine a que taxa de juros simples um capital de 500 reais, aplicado durante 10 meses, produz 150 reais de juros.
Novamente vamos anotar todos os dados fornecidos pelo enunciado do problema, pois assim teremos uma noção melhor do que deve ser feito.
J = 150; C = 500; i =?; t = 10 meses
Devemos encontrar então a taxa de juros de modo que, ao aplicar-se 500, o juros seja de 150 reais em 10 meses. Para isso, vamos substituir os dados na fórmula do juros simples:
J = C · i · t
150 = 500 · i · 10
150 = 5000 · i
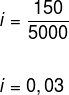
Para deixar a taxa em sua forma percentual, devemos multiplicar o número encontrado por 100, assim:
0,03 ·100
30 %
Portanto, a taxa que deve ser imposta ao capital de 500 reais, durante 10 meses, para gerar um juros de 150 reais, é de 30% ao mês.
Diferença entre juros simples e juros compostos
Existem dois regimes de juros, o juros simples e o juros composto. A diferença entre eles é que, no juros simples, a taxa de juros (i) é sempre calculada baseada no capital inicial, isto é, mesmo depois de 10 meses, por exemplo, a taxa vai ser calculada com base no capital inicial.
Já no sistema de juros composto, a taxa é calculada com base no capital inicial somente no primeiro mês, pois, nos demais, é sempre calculada com base no capital do mês anterior.
Isso faz com que o juros composto renda muito mais em relação ao juros simples. O que quer dizer que um capital aplicado durante o mesmo intervalo de tempo no regime de juros composto terá maior rendimento do que se aplicado no regime de juros simples. Para aprofundar-se nessa modalidade de juros, acesse juros compostos
Exercícios resolvidos
Questão 1 – (FGV – SP) Um capital aplicado a juros simples, à taxa de 2,5% ao mês, triplica em:
a) 75 meses
b) 80 meses
c) 85 meses
d) 90 meses
e) 95 meses
Resolução
Alternativa b. Note que o enunciado não nos fornece o valor do capital aplicado, assim vamos chamá-lo de C. A pergunta a ser respondida é: em quanto tempo esse capital triplica, ou seja, em quanto tempo teremos o juros igual a 2C, pois com o juros igual a 2C, mais o capital aplicado C, teremos o montante de 3C (triplo do capital). Assim:
J = 2C; C = C; i = 2,5% ao mês; t = ?
J = C · i · t
2C = C · 0,025 · t
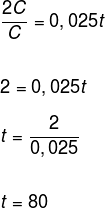
Desse modo, o tempo para que esse capital triplique é de 80 meses.
Questão 2 – Um capital foi aplicado durante 10 meses. No fim da aplicação, só de juros simples, ela rendeu seis vezes o valor do capital. Determine a que taxa foi empregada tal aplicação.
Resolução
Novamente não temos a informação de quanto foi o capital aplicado, assim vamos nomeá-lo C. No fim da aplicação, que durou 10 meses, somente de juros foi retirado seis vezes o valor aplicado inicialmente, ou seja, 6C. Temos os seguintes dados:
J = 6C; C = C; i =?; t = 10
J = C · i · t
6C = C · i · 10
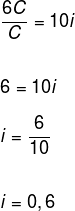
Passando a taxa para a forma percentual (multiplicando por 100), temos que:
i = 0,6 · 100
i = 60%
Portanto, a taxa aplicada nesse rendimento foi de 60%.
Juros compostos
O regime de juros compostos é o mais utilizado no mercado por oferecer maior rentabilidade financeira. Essa maior rentabilidade ocorre pelo fato de esse regime de capitalização ser calculado sempre com base no valor do montante do período anterior, o que faz com que o valor final cresça de maneira exponencial.
Fórmula do juro composto
A fórmula para calcular o valor do juro ao final de um período de tempo é a seguinte:
- M = montante;
- C = capital;
- i = taxa de juros;
- t = tempo.
Lembre-se de que o montante é sempre a soma do capital com os juros.
M = C + J
Para melhor entendermos a fórmula, vamos imaginar a seguinte situação-problema: um capital de R$ 3.000,00 foi aplicado em uma poupança durante 4 anos sob uma taxa de juros de 3% ao ano. No final desse período, qual o montante arrecadado?
| Ano | Capital (R$) | Juros (%) | Montante (R$) |
| 1 | 3000 | 3% de 3000 = 90 | 3000 + 90 = 3090
3000 · (1 + 0,03)1 = 3090 |
| 2 | 3090 | 3% de 3090 = 92,7 | 3090 + 92,7 = 3182,7
3000·(1 + 0,03)2 = 3182,7 |
| 3 | 3182,7 | 3% de 3182,7 = 95,4 | 3182,7 + 95,4 = 3278,1
3000 · (1 + 0,03)3 = 3278,1
|
| 4 | 3278,1 | 3% de 3278,1 = 98,3 | 3278,1 + 98,3 = 3376,4
3000 · (1 + 0,03)4 = 3376,4 |
Observe que o capital é sempre alterado após a capitalização. No segundo ano, por exemplo, o capital para cálculo da taxa de juros foi o montante do ano anterior. Outra observação são os valores dos montantes destacados em negrito na tabela. Veja os do terceiro ano:
3182,7 + 95,4 = 3000 · (1 + 0,03)3 = 3278,1
Nas igualdades acima, o montante destacado em roxo está escrito assim como na fórmula.
Observando a tabela acima, podemos entender melhor o funcionamento da fórmula e, consequentemente, os fatores que influenciam o valor do montante final. Para isso, basta observar quais fatores variam na tabela. O primeiro fator é o tempo, uma vez que quanto mais o tempo passa, maior é o rendimento da aplicação. O outro fator é o capital que é investido inicialmente.
Claro que a taxa também influencia o valor final do montante. Se o problema trabalhado acima mantivesse as mesmas condições e fosse alterada apenas a taxa, os demais resultados seriam diferentes.
Cálculo do juro composto
Para realizar o cálculo de juros compostos, devemos substituir as informações fornecidas pela situação-problema na fórmula, mas sempre atentos às unidades de medida da taxa de juros (i) e do tempo (t).
As unidades de medida da taxa de juros podem ser ao ano (a.a), ao mês (a.m) ou ao dia (a.d), e assim por diante. Já as unidades de medida para representar o tempo são as já conhecidas: anos, meses, dias ou horas.
O que devemos observar antes de substituir as informações é a correspondência entre as unidades de medida da taxa e tempo, ou seja, se a taxa está em anos, o tempo também deve estar.
-
Exemplo 1
Um capital de R$ 10.000,00 foi aplicado em uma poupança sob taxa de juros compostos de 5% ao mês durante 1,5 ano. Determine o valor do montante dessa aplicação.
(Dado: log1,052,466190 = 18)
Resolução
Com base no enunciado, podemos retirar as seguintes informações:
C = R$ 10.000,00
i = 5% a.m
t = 1,5 ano → 18 meses
Veja que a taxa e o tempo estão em unidades de medida diferentes. Antes de substituir na fórmula, devemos transformar uma das unidades de medida. Em geral, transformar a unidade de medida de tempo é uma tarefa mais fácil.
1,5 ano → (1 + 0,5) ano
Em um ano, temos 12 meses, logo, em meio ano (0,5), vamos ter 6 meses, assim:
1,5 ano → (1 + 0,5) ano
1,5 ano → 12 + 6 meses
1,5 ano → 18 meses
Outra observação: a taxa deve ser sempre escrita em sua forma decimal ou fracionária.
Feitas as mudanças, vamos substituir na fórmula.
M = C · (1 + i)t
M = 10.000 · (1 + 0,05)18
M = 10.000 · (1,05)18
M = 10.000 ·2,406619
M = 24.066,19 reais
Observe que, para calcular a potência (1,05)18, necessitamos do logaritmo fornecido no enunciado do exercício.
Veja que resolvendo o logaritmo a seguir, temos que:
log1,052,406619 = 18
(1,05)18 = 2,406619
Para entender melhor as operações com logaritmos, leia nosso texto específico: logaritmos.
-
Exemplo 2
Um capital foi investido em uma caderneta de poupança sob uma taxa de juros compostos de 0,6% ao mês durante um ano. Ao retirar o dinheiro, percebeu-se que o montante da aplicação foi de R$ 150.000,00. Determine o capital aplicado.
(Dados: Utilize log1,0061,074424 = 12)
Do enunciado, temos as seguintes informações:
C = ?
i = 0,6% a.m → 0,006
t = 1 ano → 12 meses
M = R$ 150.000,00
As unidades de medida do tempo e taxa estão diferentes, assim, vamos transformar a unidade de tempo de anos para meses.
1 ano → 12 meses
Agora substituindo na fórmula, temos:
M = C · (1 + i)t
150.000 = C · (1 + 0,006 )12
150.000 = C · ( 1,006 )12
150.000 = C · 1,074424
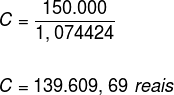
Para resolver a potência (1,006)12, é necessário utilizar o dado fornecido pelo exercício. Veja:
log1,0061,074424 = 12
(1,006)12 = 1,074424
Diferença entre juros composto e simples
A diferença entre o regime de juros simples e compostos está na forma de capitalização. No regime de juros simples, o montante do período seguinte é sempre calculado com base no valor do capital inicial, ou seja, independentemente do tempo, isso sempre vai ocorrer. No regime de juros compostos, o valor do montante é sempre calculado baseado no valor do capital do mês anterior, o que faz com que o montante cresça de maneira exponencial.
Vamos comparar um capital de R$2.000,00 aplicado em taxa de 5% ao mês durante 4 meses no regime de juro simples e composto.
Juros simples
| Juros | Montante |
| 1º mês → 2.000 · 0,05 = 100 | M = 2000 + 100 = 2100 |
| 2º mês → 2.000 · 0,05 = 100 | M = 2100 + 100 = 2.200 |
| 3º mês → 2.000 · 0,05 = 100 | M = 2200 + 100 = 2.300 |
| 4º mês → 2.000 · 0,05 = 100 | M = 2300 + 100 = 2.400 |
Observe que o valor do juros é constante – nesse caso, sempre igual a R$100.
Juros compostos
| Juros | Montante |
| 1º mês → 2.000 · 0,05 = 100 | M = 2000 + 100 = 2100 |
| 2º mês → 2.100 · 0,05 = 105 | M = 2100 + 105 = 2.205 |
| 3º mês → 2.205 · 0,05 = 110,25 | M = 2205 + 110,25 = 2.315,25 |
| 4º mês → 2.315,25 · 0,05 = 115,76 | M = 2.315,25 + 115,76= 2.431,01 |
Observe que, no regime de juros compostos, o valor do juros não é constante, pois a taxa é calculada com base no montante do mês passado. Para conhecer as propriedades e cálculos da outra modalidade de cálculo de juros, leia: juros simples.
Exercícios resolvidos
Questão 1 (IFSC) – Uma empresa financiou R$ 100.000,00 por 1 ano. O montante do financiamento foi de R$ 172.000,00. Determine a taxa de juros mensal cobrada da empresa.
Resolução
Substituindo os dados do exercício na fórmula, temos:
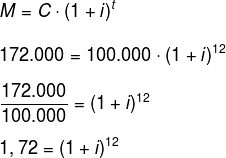
Elevando ambos os lados da igualdade a 1/12, vamos eliminar o expoente 12 localizado no lado direito da igualdade. Podemos realizar esse procedimento graças ao princípio da equivalência, o qual afirma que, se operarmos um lado da igualdade, devemos realizar a mesma operação do outro lado.
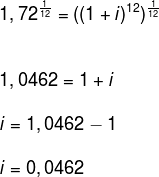
Multiplicando o 0,0462 por 100 para escrever na forma percentual, temos:
0,0462 · 100
4,62% ao mês
Questão 2 (IFSC) – Carlos aplicou R$ 20.000,00 a uma taxa de juros de 0,6% a.m e, após um tempo, verificou que o saldo estava em R$23.600,00. Determine quanto tempo o dinheiro de Carlos ficou aplicado.
[Dados: log (1,18) = 0,07188; log (1,006) = 0,002597]
Resolução
Substituindo na fórmula, temos que:
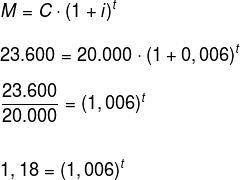
Para determinar o valor da incógnita, devemos resolver a equação exponencial utilizando logaritmos.
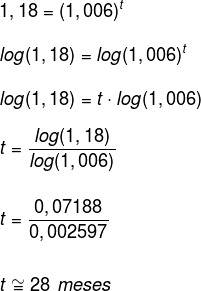
O tempo em que o dinheiro de Carlos ficou aplicado foi de 28 meses ou 2 anos e 4 meses.
Assista ao Minicurso gravado (06 de outubro a 27 de outubro de 2020):
Perícia Judicial em Contratos Financeiros
Assista as aulas
Aula 1: Conceito Financeiro da Taxa de Juros
Aula 2: Índices Econômicos para Cálculos Judiciais
Aula 3: Fundamento Jurídicos e Econômicos para Defesa do Consumidor
Aula 4: Estudo de Caso de Revisão Contratual
Veja comentários de quem já assistiu:
“Parabéns Professor, Equipe Técnica e Colegas Participantes. Muito bom o Curso”
Carlos Cardoso
“Obrigada, professor. Curso esclarecedor. Parabéns.”
Simara Queiroz
“Parabéns e muito obrigado. Foi um grande aprendizado.”
Gevasio Soares Gomes
“Excelente material de apoio.”
Ana Monica
“Parabéns pelo curso Prof. Alcides. Gostei muito da aula inaugural, bem básica, bem elucidativa e esclarecedora para aqueles que se dedicarão às perícias judiciais. Abre uma oportunidade ímpar aos consumidores e aos profissionais de economia. Eu mesmo estou implantando algo parecido e terei muito prazer de me aperfeiçoar com essas aulas. Creio que trabalharemos muito juntos em benefício da população endividada.”
Ogib Filho
“Excelente aula, Professor Alcides. Parabéns e obrigado.”
Peris Consultoria Empresarial
“Parabéns. Muito obrigado. Excelente aula.”
Prof. André Stein da Silveira
“Obrigada pelo aprendizado. Excelente curso. Parabéns ao professor e ao Cofecon.”
Christiane Alves
“Parabéns pelo mini curso professor”
Lucas Ferreira
“O curso foi muito bom. um grande aprendizado”
Maria Carolina Monteiro
“Ótimo curso professor. Obrigada.”
Jamile Melloni
“Bom mini curso”
Jocimar Pereira Roza
“Ótimo curso”
Matheus Vagner
“Obrigada”
Maria Carolina Monteiro
“Foi um bom curso. Obrigado”
Valdemar da Paixão Gomes Paixão
“Ótimo”
Raphael Amaral
“Excelente aula. Obrigado.”
Waldeatlas Barros
“Parabéns ao nosso COFECON por essa iniciativa em promover esse curso.”
Jucirlei Nazário
“Parabéns ao COFECON pela iniciativa e ao professor pela excelente aula”
Stela Balbina
“Curso muito bom. Professor está de parabéns pelo curso, didática e material de apoio.”
Ricardo Y2
“Excelentes explanações, especialmente pelos exemplos práticos apresentados”
José Carlos Neves de Andrade
